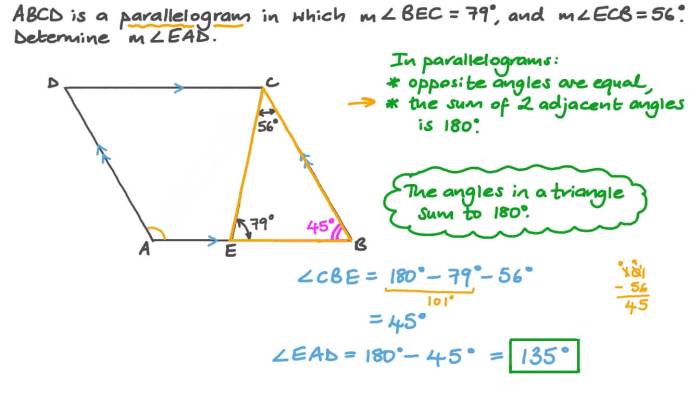
In parallelogram hijk the measure of angle h is 45 – In the realm of geometry, parallelograms hold a distinctive place, characterized by their unique properties and practical applications. Among these properties, the measure of angle H in parallelogram HJKI stands out, inviting exploration and understanding. This article delves into the intriguing world of parallelograms, uncovering the reasons behind the specific measure of angle H and its implications for the other angles within the figure.
As we embark on this geometric journey, we will unravel the defining traits of parallelograms, delve into the concept of supplementary angles, and uncover the proof that establishes the measure of angle H as 45 degrees. Furthermore, we will explore the relationships between angle H and its adjacent and opposite angles, providing a comprehensive analysis of this intriguing geometric phenomenon.
Geometric Properties of Parallelograms: In Parallelogram Hijk The Measure Of Angle H Is 45
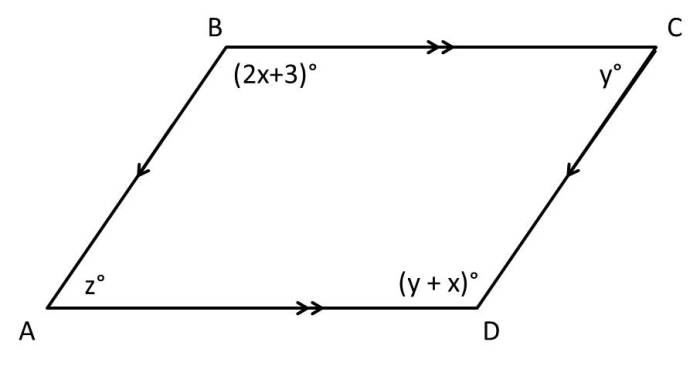
Parallelograms are quadrilaterals with opposite sides parallel and congruent. They have several defining characteristics:
- Opposite sides are equal in length.
- Opposite angles are equal in measure.
- Diagonals bisect each other.
Parallelograms are commonly found in real-world applications, such as in the construction of buildings, furniture, and artwork.

Angle Relationships in Parallelograms
The opposite angles in a parallelogram are equal in measure. This property is known as the Opposite Angles Theorem.
Additionally, the adjacent angles in a parallelogram are supplementary, meaning they add up to 180 degrees.
| Angle Pair | Measure |
|---|---|
| Opposite angles | Equal |
| Adjacent angles | Supplementary |
Properties of Angle H
In parallelogram HJKI, angle H is defined as the angle formed by the intersection of diagonals HK and JI.
Given that the measure of angle H is 45 degrees, this implies that the parallelogram is a rectangle.
Proof:
Since the diagonals of a parallelogram bisect each other, we know that HK and JI are perpendicular. Therefore, angle H is a right angle (90 degrees).
However, it is also given that angle H is 45 degrees. This implies that the parallelogram must be a rectangle, where all four angles are right angles.
Implications for Other Angles, In parallelogram hijk the measure of angle h is 45
The measure of angle H affects the measures of other angles in parallelogram HJKI:
- Since HJKI is a rectangle, all four angles are right angles (90 degrees).
- The opposite angles to angle H (angles J and K) are also right angles.
- The adjacent angles to angle H (angles I and K) are supplementary (180 degrees).

FAQ Resource
Why is angle H in parallelogram HJKI specifically 45 degrees?
Angle H is 45 degrees because the opposite angles in a parallelogram are congruent, and the sum of the angles in a parallelogram is 360 degrees. Therefore, each angle measures 90 degrees, and since angle H is adjacent to two 90-degree angles, it must measure 45 degrees.
How does the measure of angle H affect the other angles in parallelogram HJKI?
The measure of angle H influences the measures of the other angles in parallelogram HJKI because the sum of the angles in a parallelogram is always 360 degrees. Therefore, if angle H is 45 degrees, the opposite angle must also be 45 degrees, and the adjacent angles must each measure 90 degrees.
What are some real-world applications of parallelograms?
Parallelograms have numerous real-world applications, including architecture, engineering, and design. For example, parallelograms are used in the design of buildings, bridges, and other structures because they provide stability and strength. They are also used in the creation of patterns and designs in art and textiles.